


平行四边形的面积
【教学内容】人教版五年级(上)P87、P88《平行四边形的面积》
【教学目标】
1.引导学生理解平行四边形面积计算方法的推导过程,掌握计算平行四边形的面积的方法。
2.通过猜想、涂格子证明、操作验证的数学活动,让学生经历平行四边形面积计算公式的探索、推导过程,感悟“等积变换”的数学思想方法,发展学生的想象、转化、推理等空间观念,培养学生分析、概括、迁移和解决问题的能力。
3.通过一系列的数学思考和活动,让学生体会数学式思辨在数学学习中的作用,并在证明和应用的过程中感受成功的喜悦。
【教学重难点】
重点:平行四边形面积公式的推导与理解,能掌握、并能正确运用平行四边形面积计算公式。
难点:通过“转化”的方法,推导得到平行四边形面积计算公式。
【设计意图】
一、关注“测量”经验与“刻画”图形之间的联系
在小学阶段,“图形与几何”这一领域的知识包括了:图形的认识、测量、位置、平移旋转的空间变换等,《平行四边形的面积》是属于“测量”这一块。所以本次教学尝试从“测量”的经验入手——长方形的面积需测长和宽,进而引发学生内部的认知冲入:平行四边形的面积该如何测量得到,引出“证明”的数学活动。
基于“测量中必有误差”的观点,把“测量”改成“画一画”就可以很大程度上降低学生在学习中所受到的“误差”影响;另一方面,在小学阶段学习平面图形的面积,有关计算公式的教学与应用已足够重视,但“面积”对于平面图形的刻画与再认识功能却往往受到冷落,所以此次教学希望能从“测量面积”与“画图形”相联系的角度给《平行四边形的面积》教学一个新的视角。
二、关注“被探索”的误区
有一种比较普遍的现象,即教师在课堂刚开始的时候设计可供“剪、拼”的不规则图形,引导学生感知到“简——拼”这一图形操作方法,这位之后的探究活动定下了基调。有了这个铺垫的经验,学生之后的“转化”过程会比较顺利但这其中的思维含量却下降了。学生在教师事先框定的范围内进行数学活动,这样的探索是一种“被探索”。
在具体教学过程中,引入方格图。这样一来使得方格图的引入比较自然,学生自然就认为是面积单位,可以计数;二来有了方格图为背景,学生就有探究思考的基础,有利于用等积变换思想方法探索“转化”的过程。在这样的“探索”过程中,学生主动在寻找方法,而不是“借鉴”教师提供的“剪、拼”认知基础。
三、基于学生课前经验的思考。
在之前做的一些“前测”活动中,发现有不少学生课前已经知晓“平行四边形的面积=底×高”这条计算公式,那是否可以说这节课对于这部分学生失去了探索的意义和动力?
其实不然,许多学生对于“底×高”仅仅是“知道”,或是被告知过“割补”的方法,并未经历过“探索、对比、否定、证明”等过程,大脑中存在的是知识的结果而未有“过程”性的痕迹;况且,一个命题的形成,需要有一个合理化的逻辑推理过程,不只需要“正向”的思路,也需要能解释“对立面”的问题所在,这样的知识学习才是完整、有意义的。因此,这节课重点预设了学生“辩驳”的过程,在两种观点的对比中为学生留下完整的学习经验。
【教学预设】
一、旧知新引,刻画出既定面积的长方形
师:同学们画过“草图”吗?
请你在纸上画一个面积为12cm²的长方形草图,并标出必要的数据。
师:看来,要想知道图形的面积,测量边的长度再计算,是一种重要的方法。

二、凸显冲突,通过论述、辩驳、观察等过程,明理
师:长方形我们都会画,12平方厘米的平行四边形,你打算怎么画?
预设学生会有两种意见:“邻边相乘”得12,“底×高=12”。
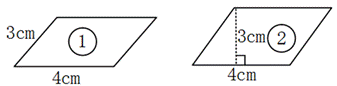
师:同样是“4×3”,它们有什么不一样吗?
1.先请①号学生阐述其观点,而后寻求“提问”;
2.展示长方形被“压”成平行四边形的过程,请学生观察其中的面积大小变化;
3.论证:原来长为4cm、宽为3cm的长方形面积是12cm²,但在“压缩”成平行四边形的过程中,面积在不断变小。所以①号平行四边形面积不是12cm²。
4.再请②号学生阐述其观点,引导学生总结“转化”的过程。
三、在方格图中证明,得出平行四边形面积的正确算法。
学习任务:在方格图中,证明②号猜想。
工具:格子图(每格代表了边长为1厘米的正方形),三角尺,水彩笔。
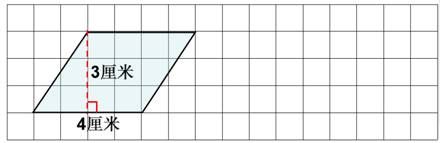
可以和同桌互相讨论、学习。
学生在此过程中发现:
1.可以通过“割——补”(即“剪——拼”)把平行四边形转化成长方形,且面积不变。
2.经“割补”得到的长方形长为4厘米,宽是3厘米,所以面积为12平方厘米。
3.转化的前后,高对应的是宽;底再经过重新拼组之后对应的是长,且长度不变。
小结:
1. “底×高”这组的平行四边形面积才是12平方厘米。
2.证明的过程中,我们发现可以把平行四边形“转化”成已经会求面积的图形——长方形,来得到平行四边形的面积。
四、经验推广,巩固“转化”方法,也证明了“等积变形”的普遍适用性。
是不是形状不同的平行四边形的面积都可以用这种“转化”的方法,变成长方形?
1.要先画出平行四边形的“高”,沿着高剪下来。
2.“变形”(转化)前、后,高对应宽,底再重新拼组后对应的是长。
五、总结,得出平行四边形面积的算法。
长方形的面积=长×宽。通过刚才的“转化”,平行四边形的“底和高”分别对应了长方形的“长和宽”,在这个过程中面积不变。
所以:平行四边形的面积=底×高,字母表示为S=a×h
六、巩固,在分层练习中留有思考的余地。
1.基础练习。
口答,计算面积。
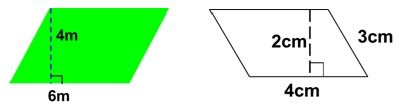
2.辨析练习。
对“单位面积”和“面积单位”的思考。
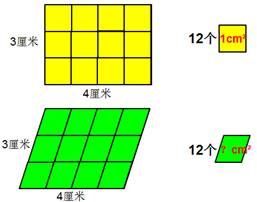
3、回到画图,你还能有什么发现?
在方格纸上(每1格表示边长为1厘米的小正方形),画一个面积为6平方厘米的平行四边形,你能画几个?你能用这些平行四边形设计出漂亮的图案吗?
作者简介:洪 侃(浙江省绍兴市越城区陆游小学,越城区教坛新秀)
