寻找中西教育的“同”与“异”

——以《发现π》《立体形状》《英国数学教学》三节课为例

写下这个题目，有些惶恐，仅凭几个课例的观察，如何能回答如此宏大的话题？但是，囿于条件，从具体案例出发，管中窥豹，或许也不失为研究问题的一种方式。于是，尝试着借助美国教师艾伦·拉斯穆森的《几何-圆：发现π》、英国教师乔安·克莉瑟若《立体形状》和杰姆森·维尔特《英国小学数学教学》这三节课，与中国小学数学教育作一个简单比较，来探讨中西方小学数学教育是否有相同的理念与实践，还有什么差异？

“同”之比较

事实上，随着东西方教育交流的逐渐深入，以及我国课程改革的推进，我们越来越感受到两者的趋同，首先我们来分享，有什么“同”？

一、重概念，拉长知识形成过程。

概念理解促进知识的探究，基于意义理解，探索公式规律，一直是我们所倡导的取向。正如艾伦·拉斯穆森《几何-圆：发现π》一课教学预案中所描述的那样，“这节课不仅交给学生π是什么，还要教给他在哪里发现”。如何发现？教师笔墨浓重、不遗余力地为学生建构了最为一般的“周长”概念，从长方形周长、三角形的周长，到不规则组合图形的周长，从篱笆、围栏、相框的周长到学生所处情景中寻找周长，从正向的“已知边长求周长”到逆向的“已知周长求面积”，由此，才逐渐进入“量圆的周长半径——求比值——找规律”的“π”探索。解读教师教学设计背后的思考，或许可以这样理解，“概念理解是概念应用的基石”，只有明确了“什么是圆周长”，之后的测量计算也就没有了困难。虽然从我们的教学进度看，学生对于“周长”、“多边形的周长计算”已是知识基础，我们推想，如果美国的学生学习圆周长之前并不具有同样的学习基础，那么，这样的推进过程，不正与我们所倡导的“基于概念理解的计算与规律探索”完全一致吗？

二、做中学，重视观察操作研究。

在活动中“学”，在“操作”中“学”，在问题中“学”，一直是西方教育的重要特征，无论是美国的《几何-圆：发现π》，还是英国的《立体形状》、《可能性思考》，三节课中，这样的特点十分鲜明。

重视操作发现。《几何-圆：发现π》一课，测量黑板上圆纸片的周长与半径、测量讲义上不同大小五个圆的周长与半径，注重操作，经历圆周率的形成过程，甚至讲这样的操作活动从课内延伸至课外，“找家里的物体测量周长与直径”，一系列的操作要求中，我们看到了“活动”在“π”意义理解中的价值与意义。

重视挑战性任务。英国教师乔安·克莉瑟若《立体形状》一课，同样重视“活动学习”，尤其值得欣赏的是，教师为学生提供了一个高认知要求的任务，“你的任务是搭建一个立方体框架，并且记录面、顶点、边的数量”，学生并不知道正方体的顶点、面、边的数量（从学生访谈发现，学生回答，搭建之前以为有8个顶点、8条边），显然，特征的发现，基于活动操作。这样的挑战任务同样运用于“方锥体（四角锥）”、“三角锥”、三角棱柱、六角棱柱的“搭建”与特征发现中，学生需要根据“立体图”想象“实物图”，不断尝试、观察、验证，获得对各类形体的特征发现。

三、重思维，关注数学能力提升

重视思维发展、重视能力提升，几乎是中国小学数学教育的精华。从英美的三节课中，我们同样能看到这样的目标落点，“运算能力”、“空间观念”、“推理能力”、“模式探讨”等等能力培养的轨迹十分清晰！试举例：

空间观念。

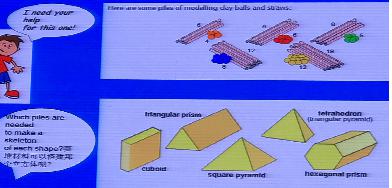
“能由几何图形想象出实物的形状”、“能形成关于几何形体的大小、形状的表象”……这些是空间观念的具体表现。英国《立体形状》一课，三个任务：“根据几何图形搭出实物”、“选择：这些形体用了哪堆材料”、“根据提示说出形状的名称”，无不指向于空间观念的发展。例如：下图任务中，学生必然需要根据形体还原想象，“有哪些面？每个面是什么形状，分别有几条边？几个顶点？”想象的基础上才能进行“边”与“顶点”材料的选择。

推理能力。杰姆森·维尔特《英国小学数学教学》一课中，推理能力、有序思考、模型推导等等思维能力的培养目标十分凸显。“比赛最终结果是1:0，那么中场结束时比分可能是多少？”“最终结果比分是1:1，中场比分可能是？”“2:1”、“3:2”、“4:2”呢？在这样的任务驱动中，学生进行推理，而这样的推理，经过教师引导，逐渐从“无序”走向“有序”，我们清晰看到了学生能力的生长与思维的变化。

四、个性化，强调个体差异指导。

活动环境轻松开放、活动指导个性充分，是我们在英美课堂中发现的又一亮点。我们看到，艾伦·拉斯穆森，用夸张的表情、煽动的语言，奔跑着示范，鼓励学生离开座位选择你喜欢的物体指一指周长，孩子们由先前的“拘谨”变得“自由”。我们看到，英美的课堂中不约而同将“糖果”作为学具，以致于孩子忍不住在搭完几何体之后开心地舔着用彩色软糖作材料的“顶点”，引发的笑声让课堂变得极其愉悦。我们看到，杰姆森·维尔特协同助教一起，对学生如何利用材料搭建出形体进行极具个性化地细致指导，让每个孩子的操作活动顺利有效。以上特点，也是我们中国数学课堂所积极倡导的方向！

“异”之探讨

当然，如果用中国小学数学教育的理念对这些课进行考量的话，或许还会发现一些差异。比如：

1. 如何增强操作的探索性？

圆周率的发现过程，依然可以看到教师指令下的“操作”痕迹，依然可以看到“先示范

操作”再“全体操作”的“传授”痕迹，依然可以看到“指名演示”时其余学生的“无所事事”。所以，笔者以为，怎样增强操作的探究性与参与性，我们的课堂会做得好一些。

2.如何还原公式的原理理解？

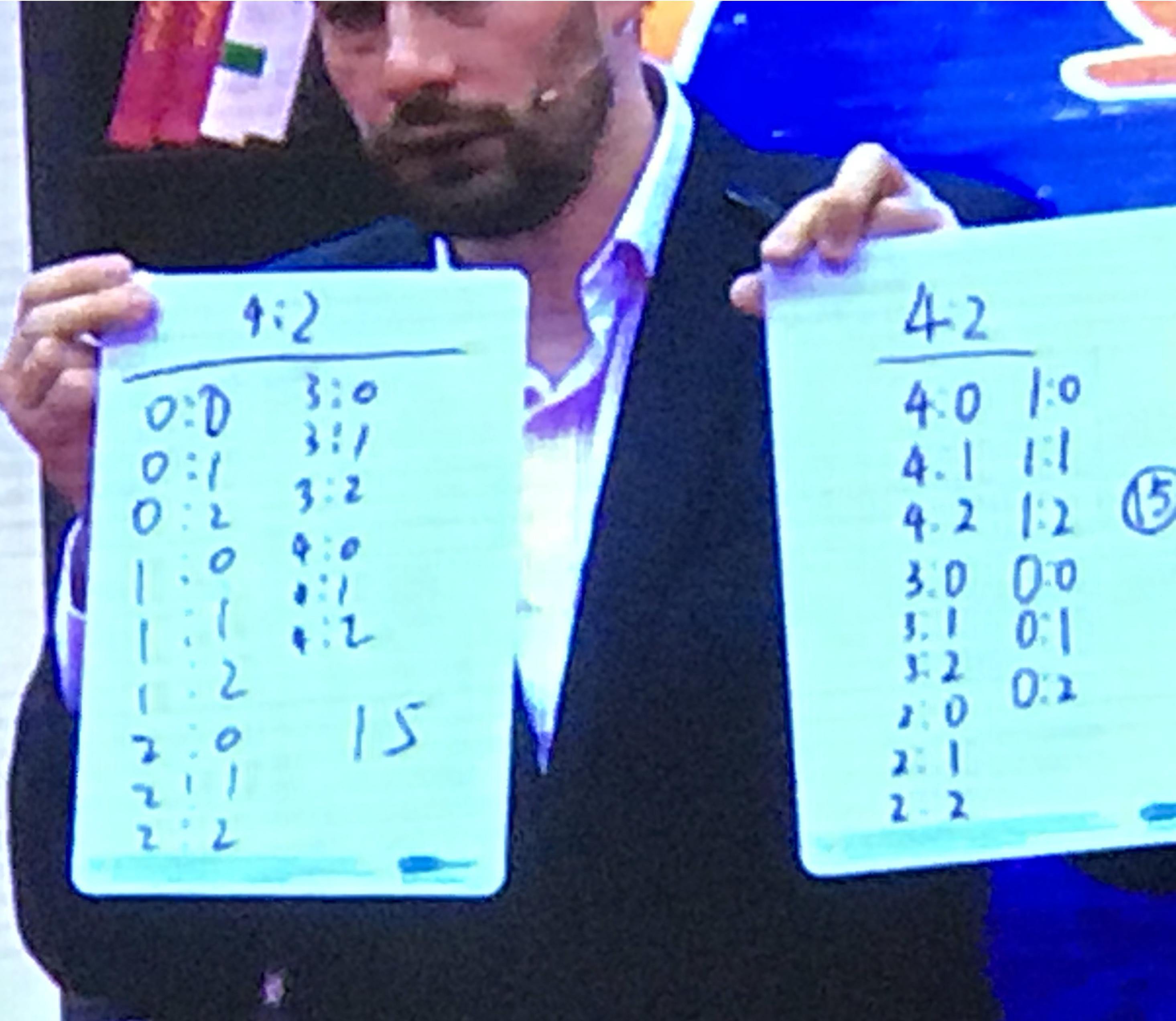
“根据比赛最终比分，推想中场时比分有几种可能”，教师引导学生思考有什么规律？“（H+1）×（A+1）=p”这样的结论得出并没有给出原理理解。如何结合学生例举的材料资源，引导思考：最终比分4:2，可能性为什么是15种？右图的学生材料不正是原理解释的最好载体吗？

最后，引用顾泠沅教授《寻找中间地带——国际数学教育改革大趋势》的一段话作为本文的结束：

寻找中西方教育的中间地带，不仅是当今数学教育的大趋势。也是整个教育改革的大策略，寻找中间地带不是简单的折中，而应以中国文化为底蕴，有机整合其他文化的教育教学取向；寻找中间地带是一种智慧，一种不走极端而达到集大成的智慧。

——《寻找中间地带——国际数学教育改革大趋势》

（作者：浙江省杭州江干区教育局教研室  潘红娟）