——看朱珊珊老师执教《梯形的面积》如何用简单的素材上出数学味

朱珊珊老师在课前做了前测：发现班上39名同学中有36名同学，在没学《梯形的面积》之前，就能用自己的方法解决问题——能独立解答的同学比例高达92%！这种严谨求实的研究态度值得我们学习。让我们想起著名认知教育心理学家奥苏伯尔说过的著名一句话: “假如让我把全部的教育心理学仅仅归纳为一条原理的话，那么，我将一言以蔽之，影响学习的惟一最重要的因素就是学生已经知道了什么。要探明这一点，并应据此进行教学。”充分暴露学情是成功教学的基础。既然没教就似乎会了，那么这节课的意义何在？思维的增量在哪里？

我们不妨深入思考一下：前测结果出来了，可以把学生分为三类：

有三个学生完全不会，我们应该怎么办？——这样的零基础，一张白纸，最好办；

一知半解的学生，我们怎么办？——找寻未知，理解原理，扶着走；

完全知道的学生，我们应该怎么办？——系统地、深刻地再经历，还可以当小老师。

听完朱珊珊老师的课，发现她在整节课的教学中有三点追求：求全、求变、求通。

一、求全

在展示求第一个梯形面积时，朱老师尽可能地让五种代表性的做法都得以展示，让全班同学不仅知道自己的做法，也了解其他同学不同的做法，打开眼界，不仅知其然，还知其所尽然。

二、求变

在展示求第二个梯形面积时，朱老师加了一点要求：尽量让别人能明白你是怎么想的？板书学生的做法：如：上底×高÷2+下底×高÷2；（下底—上底）×高÷2+上底×高；（上底+下底）×（高÷2）等等。其中对于学生较难理解的“（下底—上底）×高÷2+上底×高；”，还用微课进行了展示。

三、求联

九九归一：通过引导，学生发现：“上底×高÷2+下底×高÷2、（下底—上底）×高÷2+上底×高、（上底+下底）×（高÷2）”都可以写成“（上底+下底）×高÷2”这一通性法则。

三题对比：波利亚有言：“一个专心的、认真备课的教师能够拿出一个有意义但又不复杂的题目，去帮助学生挖掘问题的各个方面，使得通过这道题，就好像通过一道门户，把学生引入一个完整的理论领域。”俗话也说：题好文一半，秧好谷一半。那么，什么样的材料有利于学生的自主构建？

心理学表明，学生通过一定数量的有序练习比解大量无序题目更能提高学习效率和解题水平。朱老师构建一个个知识组块，而这些组块相对于孤立的知识点无疑具有更大的功能。日常生活并不能为学生提供这些经过高度结构化处理过的素材，它可以避免学生走太多的弯路，耗费太多的时间。

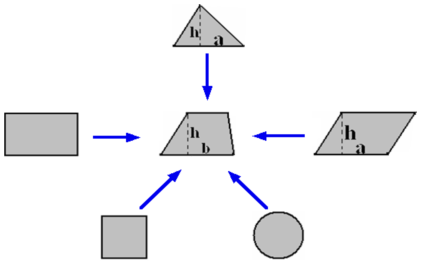
本节课一共练习求了三个梯形面积，这三个梯形之间是有着内在的联系：上底和下底虽不同，但是上底+下底的的和是相同的，高也是一样，因此面积是一样的。它们三个实际上是梯形等积变形的三种不同模样。在这个基础上，上底一直变形，变小变小，一直变到上底为0，学生恍然大悟，原来这是个三角形！三角形可以看成是一个上底为0的特殊梯形，三角形的面积公式也可以写成：（0+下底）×高÷2，即：底×高÷2——把材料用深、用透、用足了。

类推其他：有了这个做基础，让学生大胆猜测平行四边形、长方形、圆形面积，打通它们之间的关系。学生脱口而出：梯形面积是个万能公式！

这一教学环节，学生从知之较少到知之较多，从肤浅离散到深刻系统，在求变、求联的多维穿越中，瞻前顾后，学会了“融会贯通”。

乌申斯基有名言：装着一些片段的、没有联系的知识的头脑，像一个乱七八糟的仓库，主人从那里是什么也找不出来的。智慧不是别的，是组织得很好的知识体系。朱老师这样的教学就达到了知识结构化的目的，将所学知识加以归纳和整理，使之条理化、纲领化，做到纲举目张，不是像一盘散沙，要像红线串珠。当知识以层次网络的方式排列时，就可以大大提高检索效率。

最后一点点想法和大家共享：

千金难买回头看：作为数学老师，要向朱老师学习，有拎一拎，比一比，联一联的敏感和意识。

学生抄完数据和运算符号，提醒他们“千金难买回头看”——“核对一下抄写是否正确”，学生的计算正确率定会大大提高，同时，还可以积淀下严谨、负责的品质。　　

学生解完一道题，提醒他们“千金难买回头看”——“一定这样吗？”“这其中有没有规律？”“还能怎么做”，学生的观察能力、概括能力以及创新能力就能得以培养。　

课行将结束，提醒学生“千金难买回头看”——“回顾这节课的学习过程，想一想我们是怎样解决问题的？”“它和别的知识之间有何联系与区别”，过程和方法维度的目标往往就在其中达成和提升。

总之，像竹子一样一样，“先扎根后生长”，“长一节就打个结”。

在日常教学中，我们可以根据内容的内在联系，在学生能够接受的情况下，尽可能伸长“学习的触角”，对所学知识进行适当延展，让学生能收获更多“能带走”的东西。

（浙江省杭州经济技术开发区教研室  杨迎冬）